
Droplet Manipulation
2015-08-01 00:00:00 +0000
Overview
The intention of this project was to study the simultaneous levitation and manipulation of droplets. A method in which producing single droplets of the same size (~ 1 mm diameter) had to first be solved. A droplet dispensing system was created using a Firgelli linear actuator and control board, 0.5 mm glass luer lock syringe, and 26 gauge hypodermic needle. Also used was an acrylic container in which the droplets would be able to bounce and walk on. In order to view the dynamics of the bouncing droplets, a high-speed camera with lens was used, PhotonFocus MV-D1024-TrackCam and Computar 4538454 18-108mm zoom lens. Testing of the bouncing droplets was then ready to begin using the PPOD 6-DOF vibratory device, consisting of six linear actuators coupled to a rigid plate whose movement is sensed by embedded accelerometers and controlled through MATLAB. The PPOD was used to control the motion of the surface on which droplets are manipulated by generating sinusoidal vibrations in the vertical and horizontal directions. A series of experiments was conducted to determine the stability of vertically bouncing droplets for either being stable or unstable; any droplet lasting less than 3 minutes was considered unstable. A subset of the possible frequencies and amplitudes producible by the PPOD was tested for various silicon oil combinations for both the droplets and bath. The bouncing time was recorded as a function of vibration frequency and amplitude.
period_double_26hz_20A from Josh Marino on Vimeo.
Brief Discussion of Physics of Bouncing Droplets
Liquid droplets can be sustained above a vertically vibrating liquid, as was first observed in 2005 [1]. For a range of liquid and droplet parameters, a thin layer of gas is trapped between the droplet and the surface during impact [2]. If the time that the droplet is in contact with the gas layer is less than the time it takes the gas layer to thin, the droplet will rebound off the gas layer [3]. The droplet will eventually stop bouncing due to viscous losses with the gas layer, and coalesce into the liquid surface as the gas layer thins. However, if the surface is vertically vibrated, energy is added to the system during contact with the gas layer, balancing the energy lost, allowing the droplet to bounce indefinitely.
Results
Silicone oil combinations for both the droplets and bath were then tested for stability of vertically bouncing droplets. Plots were then created for 100/100, 20/1000, and 100/1000 droplets (XX/YY describes a bath of YY mPa silicon oil with a bouncing droplet of XX mPa-s silicon oil) showing the results of the vibration frequency and amplitude for either producing stable or unstable droplets, shown below. Stably bouncing droplets are indicated by green circles, unstably bouncing droplets with red circles, and blue circles indicated that the PPOD was not capable of producing the frequency/amplitude combination before the reaching a saturation voltage. Noticed from the plots of 100 mPa-s droplets, the lowest driving amplitude for producing stably bouncing droplets was around 10 m/s² or 1 g. However, for the 20 mPa-s droplets, a trend was observed in which the driving amplitude was able to be decreased for an increasing shaking frequency. This could be caused from the resonance of the lower viscosity droplets; more tests will have to be run with higher frequencies to see if this trend of decreasing amplitude continues.
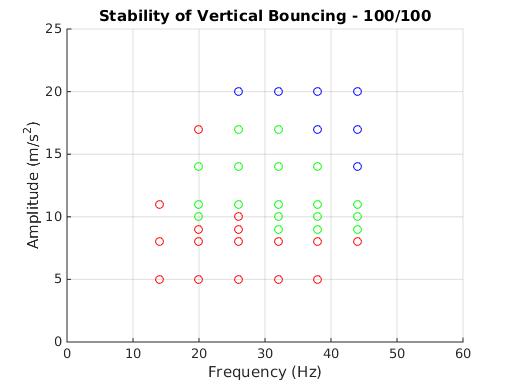
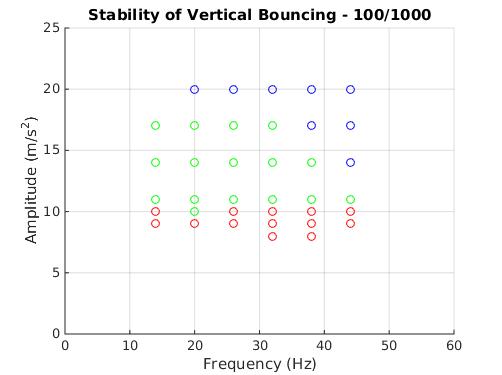
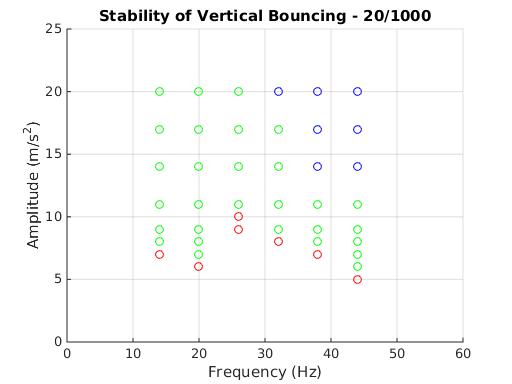
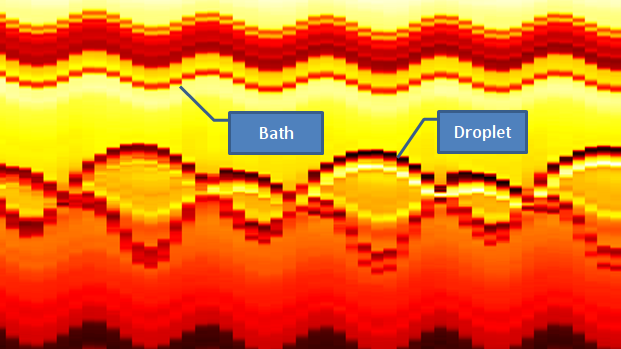
Another phenomenon observed was hysteretic bouncing for low and high bounce modes for driving amplitudes of 10 – 14 m/s². For increasing amplitudes in this range starting at the lower end, the droplet was in the low bounce mode, a short bounce followed by a longer bounce per period of shaking; however, starting at the high end and decreasing in amplitude was in the high bounce mode, a single bounce per period of shaking. Beyond this hysteretic bouncing regime, only the high bounce mode was witnessed. Another transition occurred at driving amplitude of 17 m/s² for 20/1000 and 100/1000 droplets in which period double bouncing was witnessed. In this bouncing mode, a high bounce followed by a low bounce cycle occurred for every two periods of shaking. A space time plot of the period double bouncing for a few periods is shown below, in which the droplet bouncing trajectory relative to the bath surface motion is indicated.
Also tested were 1000/1000 droplets, but droplets were not able to bounce for more than a minute. Impact velocity was very important for the 1000/1000 droplets in how far above the bath the syringe was placed. If the droplet height was too high, more than twice the diameter of the droplets, the droplets instantly coalesce. Similarly, the droplets instantly coalesce for lower frequencies due to the larger vertical displacement of the bath to achieve a desired acceleration.
Horizontal motion was briefly tested with the bouncing droplets for a frequency of 38 Hz with amplitudes of 10 m/s² in the vertical direction and 8 m/s² in the horizontal direction. Lower vertical amplitude was tested such that the droplet was in the low bounce mode allowing the droplet to be near the bath for a longer time per period of shaking. Different horizontal velocities were observed for varying combinations of droplet/bath, ranked in order of decreasing horizontal velocity: 3.05 mm/sec for 100/100, 0.81 mm/sec for 100/1000, 0.51 mm/sec for 20/1000, and 0.00 mm/sec for 1000/1000 (no horizontal displacement after 30 seconds). These results are only preliminary and need to be further tested to determine the phase relationship between horizontal and vertical bouncing.
A few other preliminary results were observed as well. First, no instant coalescences occurred for 20/1000 droplets out of 122 tests for a droplet height of 2-3 times the diameter of the droplet. This phenomenon might arise from the lower viscosity of the droplets bouncing on a very viscous fluid, allowing the droplet to deform more easily, keeping the air gap from thinning too much. Second, water droplets of 1 mPa-s were able to bounce on 1000 mPa-s bath, tested at 26 Hz for 11 and 14 m/s², with its bouncing trajectory shown below. Third, an interesting idea for horizontal motion was such that surface waves created by pushing the liquid in the bath in close proximity to the droplet caused the droplet to walk. This occurred due to the droplet bouncing on an inclined plane cause by the surface wave and rebounding with a horizontal and vertical velocity. Positioning of droplets using surface waves was tested by creating surface waves from moving a wire around in the liquid bath. Once the surface wave was close to the already bouncing droplet, the droplet walked following the direction and speed of the surface wave.
