Optimal Control - Pendulum Projectile

2015-06-01 00:00:00 +0000

Intention of Project

Intention of this project was to determine the required torques, T1 and T2, for a fully actuated double pendulum in order to release an object at the end of the second link for maximum distance thrown.

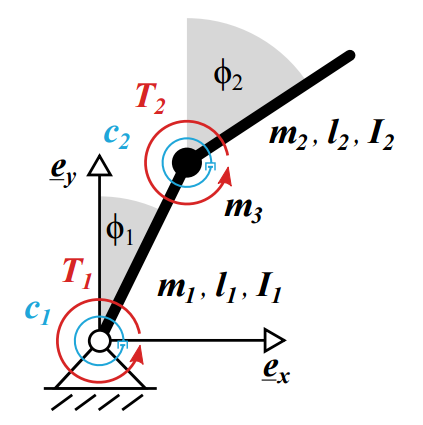
Project Details

Initial attempts to add maximum distance thrown to the cost function J(-) included directly adding distance as a function of state to the cost function. This would not have worked without recalculating the Riccati equations for steepest descent direction. Attempting to do such for a function of distance thrown involved an analytical solution from [1], of which contained multiple terms of sine, cosine, and square roots. Rather than going down that road, I attempted to alter my cost function towards one which we already had Riccati solutions.

The next attempt was trying to maximize the velocity of the end of the second link with a velocity vector 45° from horizontal, for maximum distance of a projectile. Due to the nature of a double pendulum, there are infinite configurations in which a velocity vector could be 45° from horizontal. This caused some issues when writing a cost function because the trajectory and initial conditions were irrelevant, only the terminal conditions for a specified terminal time. The closest cost function resembling this is either the LQ problem or reference tracking in which Q and R were near zero; P1 would be heavily weighted on the terminal state. Issues run into were: (1) attempting to maximize joint velocities in the LQ problem, but unable to restrain the velocity vector direction, and (2) restraining the velocity vector direction while tracking a reference, but not able to maximize the velocity, only track to a specified terminal velocity.

Due to time restrictions I had to change the focus of my project, but still decided to use a fully actuated double pendulum. The first step I took was having the double pendulum follow a continuous and differentiable function for all time t. Setbacks involved trying to figure out where my code went wrong, including going unstable for certain choices of time T, matrices Q, R, P1, and not entering the Armijo line search to find a descent direction of suitable size. Unfortunately, this took up most of my time since I was unsure of where the problem was arising, either an error in my code (which I thought it was for a long time, was one major error I did not find for a while) or going unstable because of design decisions. Eventually I was able to have the double pendulum follow any smooth trajectory for any time duration T.

The next step was the addition of a barrier function to my cost function J(-) inside the integral, as well as to the directional derivative. Barrier function for the control input, torques, was used in which the control input was raised to the power eight, (U/4)^8. This essentially would constrain both torques at each joint to ±4 N-m (CW/CCW), which was appropriate for my link lengths and masses. Initial iterates showed that the torques were being constrained, but that the reference tracking was poor. For the next couple iterates, the reference tracking was similar, but the torque spiked as much as three to five times for fractions of a seconds. After this occurred, Mathematica produced errors while trying to working on the next iterate. Due to time constraints, I was not able to find a solution to the problem. However, I did trying changing the Q, R, P1 matrices, as well as the initial guesses to xi and xibar without avail. A solution is possible since 4 N-m of torque allows the double pendulum to complete a full rotation of 360° degrees.

Future Work

Future work includes figuring out how to work with the barrier function to limit the torque output. Once that problem has been solved, I would like to work with some variant of the double pendulum throwing task. The simplest method I was able to conceive involved maximizing the velocities of both joints while choosing a variety of predetermined angles that satisfies the velocity vector at the end of the second link being 45° from the horizontal.

References

[1] Thandiackal, R.; Brandle, C.; Leach, D.; Jafari, A.; Iida, F., “Exploiting passive dynamics for robot throwing task,” Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on , vol., no., pp.2443,2448, 7-12 Oct. 2012